Linear Regression

06 Oct 2018

Linear Regression — Summarised

There are several online resources to teach yourself skills and this is especially true with computer science fields such as machine learning. One such popular resource is the Introduction to Statistical Learning: with Applications in R. It covers many of the modern and widely used statistical learning algorithms.

This ISLR series will cover the key concepts and highlighted summary of each chapter in the book. This should help provide a high-level notion of each algorithm covered and could be useful for anyone that wants to quickly refresh their memory.

Linear regression provides a “very simple approach to supervised learning” and is “useful for predicting a quantitative response”.

“selective focus photography of graph” by M. B. M. on Unsplash

Simple Linear Regression

As the name suggests, linear regression is a straightforward method of predicting the value Y based off of a single predictor *X *and it assumes an approximately linear relationship between the two represented as follows:

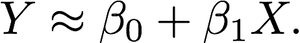
Where β₀ and β₁ are knowns as coefficients or parameters. Once the model coefficients have been learned from the training data, they can be used to make predictions.

It is useful to assess the accuracy of the model by minimizing the “error” produced. One way to measure this error is the *residual sum of squares (RSS) *which is defined as follows:

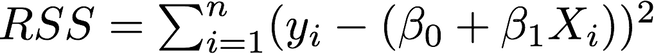
The least squares approach chooses coefficients to minimize the RSS. Using some calculus, one can show that the minimizers are:

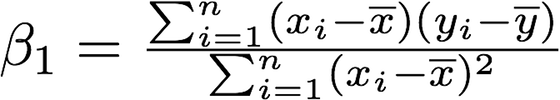
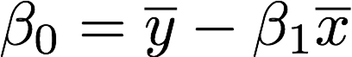
Where the overline above *x *and *y *represents the mean of those respective columns.

It’s easy to expand this model to capture multiple predictors and even non-linear predictors such as exponential or polynomial expressions. However, with increasing number of predictors of higher order one needs to be careful about overfitting the data.

Assessing Accuracy

Residual Standard Error: The RSE is an estimate of the standard error deviation of ε (unavoidable error or noise). This can also be explained as the “average amount that the response will deviate from the true regression line”.

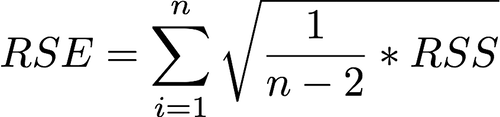Residual Standard Error

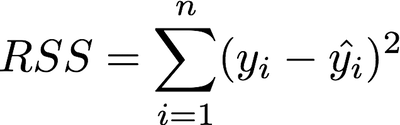Residual sum of squares

R² Statistic: The R² measure provides more of a “proportion” since it always takes a value between 0 and 1 as compared to RSE which is measured in units of Y.

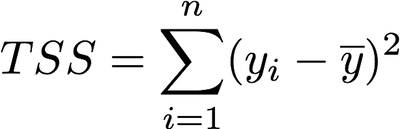Total sum of squares

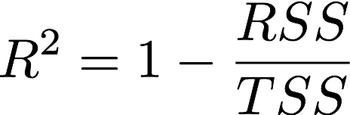
Some important questions to consider while developing a linear regression model:

• Which of the predictors in X *are useful in predicting *Y?

• How well does the model fit the data?

• Given a set of predictor values, what response values should we predict?

As always for more detailed concepts and examples please refer to the book. The book also includes lab assignments where you can implement the models you learn in each chapter in R.

If this post receives a positive response I will continue to summarize other chapters in ISLR which include other useful machine learning models like: K-means Clustering, SVMs as well as Decision-Trees.